격자상에서 전개되는 "죄수의 딜레마" 게임
Spatialized Prisoner's Dilemma 다운받기
1. 죄수의 딜레마의 의미와 그 전략들 그리고 연관 소프트웨어에 대해서는 앞서 소개했다. 지금 소개하고자 하는 것은 사각형의 격자상에서 전개되는 죄수의 딜레마 -넓은 의미에서- 게임이다. 이것은 죄수의 딜레마를 세포자동자의 형식으로 변환시킨 것이라고 볼 수 있다.
바둑판의 격자 구조상의 각 셀들은 게임 당사자(agent) 들이다. 이 셀들은 인근 셀들에 대해 협동(cooperate)과 배반(defect)의 2가지 전략을 구사한다. 배반과 협동에 대해서 득점표에 따라 점수가 주어지며 각기 다음 세대에 인근한 셀(인근의 범위는 몇가지 있지만 세포자동자의 표준에 따라 통상 무어이웃을 사용한다.)들 가운데 가장 높은 득점을 얻은 셀의 전략을 따른다. 배반에 대해서는 붉은 색을, 협동에 대해서는 푸른 색을 사용한다. 배반 전략을 택한 셀이 높은 득점을 하면 인근의 셀들은 다음 세대에 모두 붉은 셀로 바뀐다. 이 과정에서 협동에서 배반으로 또는 배반에서 협동으로 전략을 바꾸는 셀들이 나온다. 이것을 표현하기 위해서 전자의 경우는 노란색을 후자의 경우에는 초록색을 사용한다. 여기다 협동과 배반의 푸른색과 붉은색을 합하면 결국 4가지 색깔의 색채순환이 일어나는 셈이다. 얼핏 생각하면 배반전략이 유리해서 빠른 시간안에 붉은 색으로 칠해질 것으로 보인다. 그러나 배반전략은 자신안에 폭탄을 안고 있어 스스로 자멸하는 경우가 많다. 이렇게 해서 어느 하나가 일방적 우세를 점하지 못하고 그 둘 사이를 진동하게 된다. 모니터 상에서는 이 네가지 색깔들이 진동하면서 현란한 패턴을 만들어 내는데 이것이 "죄수의 딜레마 격자 게임"(Spatialized Prisoner's Dilemma)이다.
2. 이 게임에서 가장 기본적인 것이 "득점표"(payoff matrix)와 "인근"(neighborhood) 그리고 "이행규칙"(transition rules)의 규정이다. 득점표에 대해서는 오리지날 죄수의 딜레마 게임과 동일하다. 표준 득점표는 아래와 같다.

괄호안의 좌측은 a의 값이고 우측은 b의 값이다. a와 b의 값은 대칭이므로 통상 득점표는 a값만 나타낸다.(행row만을 표기한다) 아래와 같이 나와 있는데 이것은 정확히 위의 의미이다.

여기서 협동-협동, 배반-배반, 협동-배반, 배반-협동의 4가지 전략이 가능한데 상호협동은 약자 R(reward), 상호배반은 P(punishment), 협동-배반은 "착취당했다"는 의미에서 S(sucking)으로 그리고 배반-협동은 달콤한 유혹이라는 의미에서 T(temptation)으로 표기한다.

Parameters→Payoffs/Initialization을 선택하면 득점(payoffs)을 규정하는 박스가 나온다. 득점 할당이 T>R>P>S 가 되면 전형적인 죄수의 딜레마 게임이 된다. 그러나 이 값을 약간 다르게 조정함으로써 여러 다른 양상들의 게임이 출현한다.
payoffs의 상단에 Number of Strategies가 있다. 디폴트값이 2로 되어 있다. 이 경우 2^2 의 전략이 가능하다. 앞서 협동-협동, 배반-배반, 협동-배반, 배반-협동 등 4종이 그것이다. 3을 주면 2^3 = 8개의 전략이 가능하다. 3을 선택하는 순간 아래 득점표가 8칸으로 활성화되는 것을 볼 수 있다. 4의 경우 16개의 전략이 가능하다.
그 하단의 Geometry는 이 격자구조의 모양에 대한 규정이다. Toroidal은 화면의 상, 하를 둥글게 말아 연결시킨 다음 좌, 우를 다시 말아 연결시키면 생겨나는 도넛츠형 구조이다. Cylindrical은 좌, 우만을 연결시킨 것으로 그렇게 되면 실린더 형태가 된다.
다음은 인근의 규정이다. Parameters→Transition Rules를 선택하면 Neighbourhoods가 나오고 거기에 Standard와 Large가 있다. Standard는 자신과 그리고 자신의 직접 인근 그래서 3×3 = 9개의 셀로 된 무어이웃을 의미한다. 한편 Large는 5×5 = 25개의 셀을 이웃으로 한다. 후자를 선택할 경우 계산량이 많아 속도가 아주 늦어짐으로 선택하지 않는 것이 좋다.
우측에 Learning이 있다. 이것은 각 셀이 인근 셀들 가운데 가장 좋은 전략에 자신의 전략을 동조시켜 나가는 방법에 대한 규정이다. Imitate Best Neighbour는 인근셀 가운데 가장 득점이 높은 셀의 전략을 따르는 것이다. 결국 득점력이 높은 전략으로 채워지는 것이기 때문에 적자생존의 자연선택에 대한 그럴듯한 모사이다. 그러나 현재의 득점력이 미래의 득점력을 보존해 주지 않으며 무엇이 "좋은" 전략인가 하는 것은 전체 문맥에 의존하는 고도로 상관적인 것이다. 그래서 단순 득점에 근거해서 최적자(the fittest)를 구하는 Imitate Best Neighbour의 방법은 지나치게 단순무식하다. 이 소프트웨어는 이 방법을 넘어서서 "좋은" 전략을 판단하는 여러 가지 옵션들을 제공하고 있다. 필자는 이 단순한 전략의 이해에도 급급해서 다른 전략들을 이해하기에는 역부족이다. 누군가가 좀 보완해주었으면 좋겠다.
3. 여기서의 필자의 목적은 좋은 전략이 무엇인가에 대해 검토하는 것이 아니고(필자로서는 역부족이다.) 도대체 Spatialized Prisoner's Dilemma가 어떻게 작동하는가를 이해하는데 있다. 패턴들이 모니터상에서 어지럽게 난무하는 모습을 보고 이것이 죄수의 딜레마와 무슨 상관이 있는지 이해가 되지 않았다. 이 소프트웨어를 통해서 최소한 그것이 어떻게 작동하는가는 이해할 수 있게 되었다.
화면을 열면 푸른색 바탕에 빨간 점이 중앙에 찍혀져 있다. 물론 이것은 Parameters→Payoffs/Initialization→Initialization Method에서 One Foreground가 디폴트로 지정되어 있기 때문이다. 그 아래에 Foreground, Background가 있다. 그 값이 1, 0 으로 되어있다. 좌측의 Payoffs를 보면 0은 cooperate로, 1은 defect를 가리킨다는 것을 알 수 있다. 그리고 앞서 cooperate는 푸른색, defect은 붉은색으로 지정되어 있다고 했다. 결국 초기화면은 푸른색 바탕(Background=0)에 붉은색 점(Foreground=1) 하나가 찍혀 있는 모습이다. 연습삼아 그 값을 0, 1로 바꾸어 보라. 붉은 바탕에 푸른점 하나가 찍혀져 있을 것이다. 그외 몇가지 옵션들이 있는데 이해하기 어렵지 않을 것이다. (선택결과가 모니터상에 나타나지 않는다고? 툴바 가운데 초기화 단추인 I를 눌러야만 선택결과가 업데이트된다.)
푸른색 바탕에 붉은 점, 이것의 의미는 무엇일까? 협동자들의 세계의 한 가운데로 침투해 들어온 배반자의 모습이다. 거짓말을 할줄 모르는 셀들 사이로 끼어 들어온 거짓말쟁이 셀이다. 이 사기꾼은 이 순진한 셀들을 등쳐먹으면서 급속히 퍼져나갈 것이다. 조만간 모니터를 붉은 핏빛으로 물들인 묵시록적 미래가 출현할까? 그렇지 않다는데 세상의 오묘한 이치가 있다. 사기꾼이 득세하면 사기꾼이 사기꾼을 만날 가능성이 많아진다. 그리고 순진한 자에게 효율적이던 그 기술은 사기꾼 앞에서는 아무 장점도 되지 못한다. 여기서 사기꾼의 증식에 제동이 걸리게 되고 그 틈새로 다시 협동자들이 부활한다. 자 이제 ▶▶을 눌러 이 세계의 결말이 어떻게 전개될지 보기로 하자. 붉은 색 일변도로 쉽게 가지 않을 것이다.
이제 이것이 작동하는 원리를 알기위해 번거롭더라도 수작업으로 변화를 추적해 보자. Parameters→Payoffs/Initialization에서 득점표의 초기값이 1, 0.6, 1.9, 0으로 주어져 있다. 좀 단순화하기 위해 0.6을 0으로 바꾸어 득점표를 1, 0, 1.9, 0으로 두자. 아래는 수작업으로 4세대 까지 계산해본 결과이다.
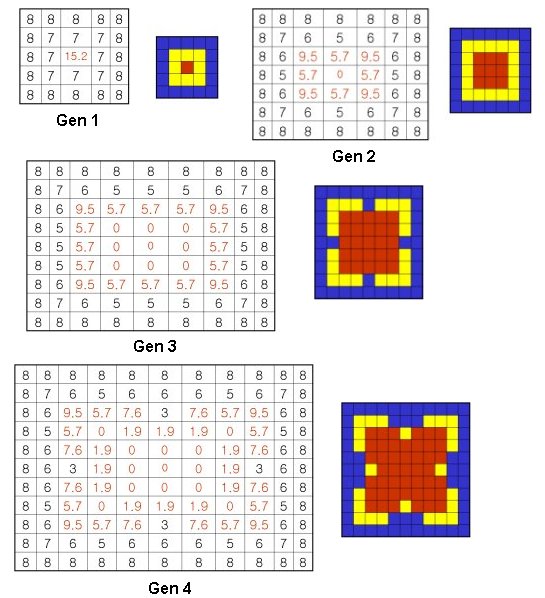
1세대를 보자. 중앙의 붉은 셀은 배반자 셀이다. 무어이웃을 택하고 있으므로 인근의 8개의 청색셀과 대결한다. 청색셀은 협동카드를 내고 붉은 셀은 배반카드를 낸다. 붉은 셀은 득점표에 따라 경기당 1.9점을 득점한다. 8개의 셀이 있으므로 전체 득점은 1.9×8 = 15.2 점을 득점한다. 붉은 셀 인근의 8개 푸른 셀은 붉은 셀과의 경기에서만 0점을 얻고 나머지 셀과는 서로 협동함으로 각 1점, 합 7점을 얻는다. 그 바깥의 셀들은 모두 청색셀과 이웃하고 있다. 서로 협동함으로 모두 8점씩을 얻는다.
이제 이 계산결과를 무늬패턴으로 바꿔보자. 단순 무식한 Imitate Best Neighbour을 선택한다. 이것은 각 셀이 무어인근안에서 가장 득점력이 높은 셀의 색을 취한다는 규정이다. 붉은 셀 인근의 7개의 셀은 모두 붉은 셀의 영향권안에 있다. 그렇다면 그 모두는 가장 득점력이 높은 셀(17.2의 붉은 셀)의 색을 취하게 될 것이다. 그것은 붉은 색으로 이행할 것이다. 그런데 노란색으로 되어 있다. 이것을 이해하기 위해 앞서 소개한 색순환규정을 다시 한번 상기하자.
통상 배반에 대해서는 붉은 색을, 협동에 대해서는 푸른 색을 사용한다. 배반 전략을 택한 셀이 높은 득점을 하면 인근의 셀들은 다음 세대에 모두 붉은 셀로 바뀐다. 이 과정에서 협동에서 배반으로 또는 배반에서 협동으로 전략을 바꾸는 셀들이 나온다. 이것을 표현하기 위해서 전자의 경우는 노란색을 후자의 경우에는 초록색을 사용한다. 여기다 협동과 배반의 푸른색과 붉은색을 합하면 결국 4가지 색깔의 색채순환이 일어나는 셈이다.
협동에서 배반으로 이행하는 셀은 일단 노란색을 취한다. 다음 세대에서도 배반 전략을 그대로 유지하면 그 때 빨간색으로 바뀐다. 그래서 세대1의 우측의 패턴이 만들어진다. 컴퓨터로 그 결과를 확인해 보자.(한 단계씩 보고자 할 때는 ▶을 사용한다.)