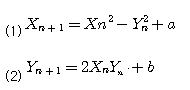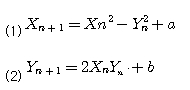카오스
1. 상호되먹임과 비선형성
2. 로지스틱맵 식
3. 로지스틱맵 그래프
4. 파이겐바움 수와 프랙탈적 특성
5. 만델브로트 맵
6. 만델브로트식과 복소수공간
7. 만델브로트 우주에로의 유영8.실행 소프트웨어
선형이란 두 양 사이의 정비례 관계에 기초하여,그래프에서 직선으로 나타낼 수있는 모든 종류의 거동을 나타내는 수학용어이다. 선형적 계의 작용은 계를 이루고 있는 각 부분들의 거동의 합으로 나타낼 수있지만 ,비선형적 계의 거동은 이러한 합 이상의 것이다. 선형계와 비선형계의 차이는 보통 가정에서 사용하는 팬 히터와 원자폭탄을 비교하여 쉽게 설명할 수있다. 팬 히터 2개를 사용하면 2배의 열을 얻을 수있고,3개를 사용하면 3배의 열을 얻을 수있다. 이와같은 양상은 열의 양과 히터 사이의 선형적 관계를 나타내 준다. 원자폭탄의 경우 연쇄반응을 일으키고 이것이 다시 열발생을 증폭시킴으로써 더욱 폭발적인 연쇄반응을 유도한다. 이것을 '양(陽)의 되먹임'(positive feedback)이라 하는데 전형적인 비선형성을 보여주고 있다.
되먹임의 방식은 어떤 식에 의해서 산출된 값을 다시 그 식속에 대입하는 것이다. 간단한 되먹임의 예로 Xn+1 = 2Xn 의 방정식을 살펴 보자. 이것을 반복점진식으로 프로그램하면 다음과 같다.
10 X = 1
20 PRINT X;
30 X = 2X
40 PRINT X;
50 GOTO 30
60 END
Xn(n=1)이 1이면 Xn+1은 2가 된다. 이어서 2,4,8,16,32,64....로 이 수열은 산출된다. Xn을 1.5에서 시작하면 3,6,12,24,38....의 수열이 나타난다. 여기까지는 비선형적인 성질은 전혀 없다. 이제 좀더 긴 초기값을 취해 보자. Xn(n=1)이 0.5986이면 Xn+1은 0.1972이다. 앞의 정수 부분은 버리고 소숫점 이하의 부분만 취해서 계산해 보면 다음과 같은 수열이 도출된다.
5986,1972,3944,7888,5776,1552,3104,6208,2416,4832,9664,9328,8656,.....
이것은 아무 규칙성 없는 산발적인 수의 나열 처럼 보이지만 일정한 패턴이 반복된다. 예컨대 Xn(n=1)이 0.707070일 경우 17회 반복되었을 때 이 숫자가 도로 나타나고 다시 동일한 수열이 반복된다. 일반적으로 유리수의 경우는 숫자의 길이에 따라 주기의 차이는 있지만 궁극적으로는 반복되는 패턴이 나타난다.
지금 예로 들은 식은 간단히 배가(倍加) 시켜나가는 것이지만, 이것보다 약간 복잡한 페어홀스트(P.F.Verhulst)의 식 -통상 로지스틱 사상(logistic map)이라 부른다- 의 경우를 보자.
Xn+1 = B Xn(1-Xn)
이것은 앞서의 식 Xn+1 = B Xn 에 부가적인 항 (1-Xn)을 첨가한 것이다. B를 2로 두고 이것을 다시 쓰면 다음과 같다.
Xn+1 = 2(Xn - Xn × Xn)
Xn이 두번 곱해져 있다. 여기서 패턴의 반복을 찾아낼 수있을까? 숫자의 길이에 따라 주기가 길어지는데, Xn(n=1)이 0.707070일 경우 다음 반복에서 2×(0.707070 - 0.707070 × 0.707070)이 되어 소숫점 이하 10자리,다음 반복에서는 20자리,40자리로 등비급수적으로 불어나갈 것이다. 여기서 새로운 패턴이 시작되는 주기를 찾아내기란 거의 불가능하다. 여기서 예측불가능한 비결정론적 세계가 나타난다.
이 식은 1845년 페어홀스트가 인구증가를 수학적으로 나타내기 위해 도입한 식이다. 수효증가를 나타내는 방정식을 비선형으로 만든 그의 개념은 인구증가의 과정을 아주 간략하고 효과적으로 표현하고 있다. 여기서 Xn=1은 개체수의 가능한 최대수,즉 100%를 나타내고,Xn=0.5는 그것의 절반 50%를 나타낸다. 이 식의 의미를 수치를 넣어 구체적으로 검토해 보자. 이것을 위해 다음과 같은 반복점진식을 프로그램했다.
10 INPUT R
20 X = 0.9
30 N = 1
40 PRINT X;
50 N = N+1
60 X = R*X*(1-X)
60 PRINT X,N;
70 GOTO 50
80 END
여기서 x의 값은 식 전체의 형태에 본질적인 영향을 주지 않는다. 처음에는 x의 값에 따라 차이가 있지만 반복의 횟수를 늘이면 똑같은 형태를 보여준다. 예컨대 x=0.9와 x=0.02이고,r=1.5일 경우를 비교해 보자. x=0.9일 경우 0.9,0.135,0.1751,0.2167(소숫점 4자리 까지만 나타내겠다)...로 변하다가 25회 반복 후 26회째(n=26) 0.3333으로 수렴한다. x=0.02는 0.02,0.294,0.0428...로 변하다가 30회째 0.3333으로 수렴해서 x=0.9일 경우와 같아진다. 이것은 수식의 형태로 보아 예측될 수있는데 x값이 증대하면 (1-x)값은 감소하도록 되어있어 그 곱은 두 값의 크기에 큰 영향을 받지 않는다.
그러므로 편의상 x를 0.9로 두고(x=0.9),r의 값의 변화에 따른 x(1-x)의 변화를 추적해 보자. r=2.3일 경우 9회째 0.5652(약 57%)에 정착하고 그 이후의 반복계산에서는 더 이상의 변화를 보이지 않는다. r=2.4일 경우 10회째 0.5833에 정착한다. r을 높이면 이 값은 점점 높아져 r=2.5일 경우 25회째 0.6(60%)에 고정된다. r=2.98일 경우 처음에는 일정한 수렴을 보이지 않고 불규칙적으로 변화하다가 354회째에 0.6644에 고정된다. 결론적으로 r이 2이하일 경우 특정값에 수렴되는 일정한 규칙성을 보인다.그러나 r=3일 경우 새로운 현상이 나타난다. 0.6644에 있던 끌개(attractor)가 불안정해져서 불규칙적인 값을 산출하다가 1683회 반복후 0.6723과 0.6609의 두개의 끌개로 나뉘고, 그 이후는 이 두 값 사이를 교대로 진동한다. r=3.2가 되면 21회째 부터 0.5130,0.7994 사이를 진동한다. 이것을 '갈래질' 또는 '분지'(分枝;bifurcation)라고 하는데 여기서 두개의 가지가 나타난다는 것을 의미한다.
이것을 r=3.5로 높이면 이 두 값이 다시 불안정해지면서 불규칙적 양상을 보이다가 31회째부터0.8749,0.3828,0.8269,0.5008사이를 진동하는 4개의 새로운 갈래질이 발생한다. 이것이 3.56에 이르면 또다시 불안정해져서 8개의 갈래질이, 3.567에서 16개의 갈래질이 발생하고,뒤이어 32,64,128...의 갈래질이 나타나는 소위 '주기배증'(週期倍增;period-doubling)이 가속되다가 3.58 부근에서 갈래질은 무한대가 된다. 이것이 바로 혼돈상태(chaos)이다.
3. 로지스틱맵 그래프
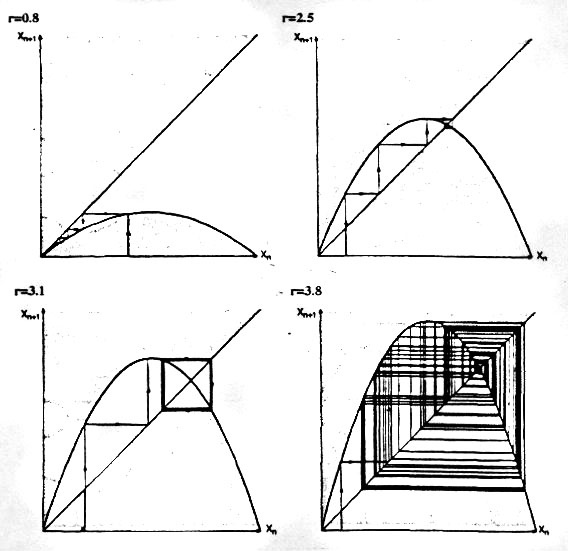
이것을 r과 x간의 관계가 아니고,Xn과 Xn+1간의 관계로 나타내면 r값에 따른 소멸,수렴,혼돈의 관게를 잘 보일 수있는데 다음 도표는 그것을 보여주고 있다.(그림1) 여기서 각각의 y값(즉 Xn+1)은 새로운 입력치로서 다시 x값에 재입력되기 때문에 그 궤적은 45도의 직선 즉 y=x의 직선상에서 반사된다. 이 그림은 소멸,수렴,혼돈이 포물선의 가파른 정도(즉 r값의 크기)에 민감하게 영향을 받는다는 것을 보여준다. 봉우리가 너무 낮은 함수(r=0.8)는 x의 초기값이 얼마이든 간에 결국 소멸되어 간다는 것을 보여준다. 가파란 정도를 증대시키면 안정된 일정한 점으로 수렴해 간다.(r=2.5) r이 어떤 값을 넘어서면 두 갈래질 사이를 진동한다.(r=3.1) 그리고 갈래질이 계속되다가 마침내 궤적은 일정한 진동을 보여주지 않는 카오스의 상태로 변한다.(r=3.8)
<그림1> Xn=rXn(1-X)의 그래프. 여기서 r값에 따라 포물선의 경사가 달라짐을 볼 수있다.
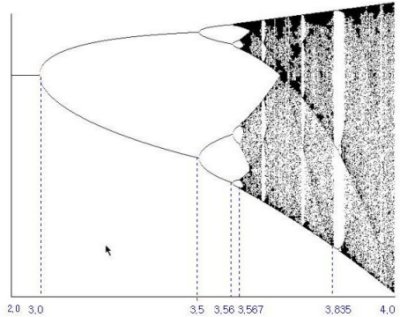
이 식의 의미를 좀더 자세히 검토해 보기위해서 이것을 r대 x의 그래프로 그려 보면 다음과 같다.(그림2)
<그림2> r의 크기에 따라 무수한 갈래질이 일어나고 있는 모습
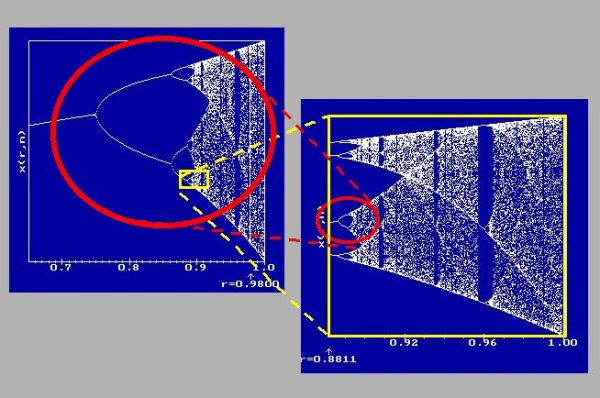
이것이 이야기의 전부가 아니다. 무수한 갈래질을 치던 혼돈의 양상 너머로 갑자기 규칙적 질서가 출현한다. 컴퓨터 그래픽을 통해 보면 이것을 확인할 수있다.
위의 도표에서 점으로 가득 채워져 있는 검은 부분은 한 계가 발견될 수있는 상태가 무한대임을 나타낸다. 이것은 전혀 예측할 수없는 혼돈의 상태임을 의미한다. 그런데 여기서 수직으로 나타나는 흰 띠들을 볼 수있을 것이다. 이것은 혼돈속에 간헐적으로 출현하는 규칙성을 나타내고 있다. 예컨대 r=3.835에서 50회 정도의 반복계산 동안 예상대로 혼돈의 양상을 보이다가 57회째 갑자기 0.5120,0.4945,0.5863이 차례로 반복되는 셋갈래질의 질서가 출현한다. 그리고 r=3.739에서 혼돈 후에 119회째 갑자기 0.8411,0.4996,0.9347,0.2280,0.6582이 차례로 반복되는 다섯 갈래질의 질서가 출현한다. 혼돈속에 존재하는 이러한 질서를 '간헐성'(intermittency)이라 한다. 이 간헐성은 혼돈속에서 새로운 질서가 자발적으로 생성될 수 있음을 보여주고 있다.
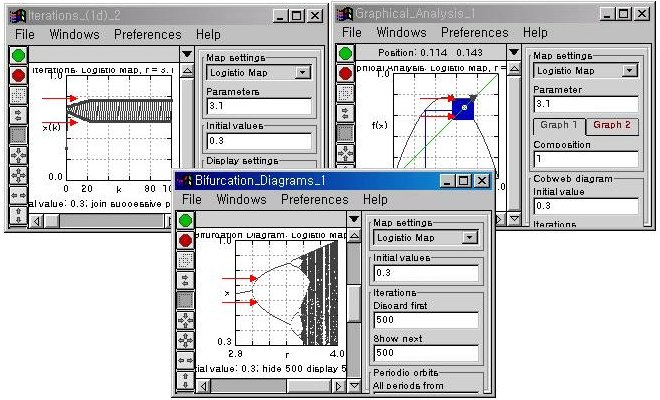
이것을 확인해 볼 수 있는 좋은 애플릿을 소개한다.아래 그림은 그 애플릿을 실행한 결과이다.
http://sunsite.anu.edu.au/education/chaos/Download.html
상단의 좌측 그림은 r=3.1 로 두었을 때 x가 두 값(0.752와 0.571;빨간색 화살표로 표시한 값 )사이를 순환하고 있음을 보여준다.이것을 직관적으로 보여주는 것이 상단의 우측 그림이다.이것을 다시 r대 x의 그래프로 그린 것이 하단의 그림이다.소프트웨어에서 r값(좌측파넬의 parameters)을 다른 값으로 바꾸어 봄으로서 하단의 그래프가 어떻게 만들어지는가를 확인해 보자.그리고 초기값(initial values)을 바꾸어도 전체 형태가 변하지 않음도 확인하자.
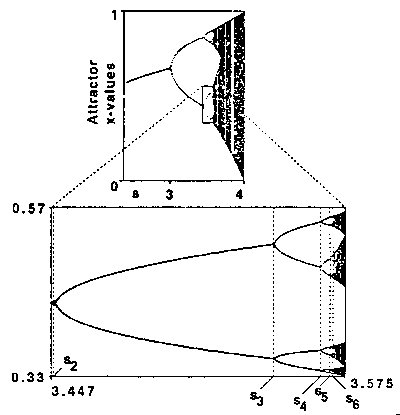
1970년대 파이겐바움(M.Feigenbaum)은 이 로지스틱맵에 들어있는 중요한 사실을 발견했다.즉 그것이 어떤 종류의 로지스틱맵이든 상관없이 혼돈으로 향하는 주기배증경로에 보편적 특성이 들어있다는 것이다.다음 그림을 보자.
일반적으로 k가 커짐에 따라 4.669201690...에 접근해 간다. 이것은 로지스틱맵이 프랙탈적 속성을 갖고 있음을 의미한다.
<그림4>로지스틱 맵에 있어서 전체와 부분의 프랙탈적 상사구조
만델브로트맵은 다음 식으로 표현되는 2차원 동력학계이다.
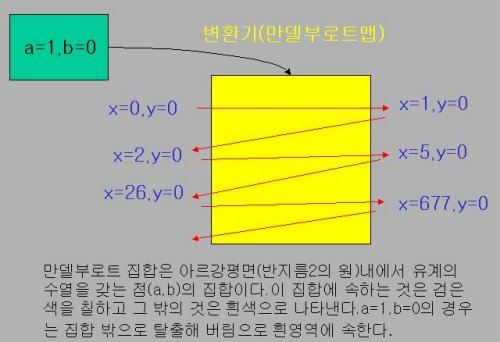
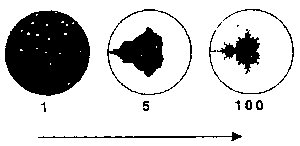
이것은 일종의 변환기라고 볼 수 있다. 이 변환기에 어떤값(a,b)를 넣어을 때 어떤 값이 나오는지를 조사해 보자.a=1,b=0의 경우는 어떨까? 결과는 (0,0),(1,0),(2,0),(5,0),(26,0),(677,0)...으로 무한대로 증가한다.
<그림5>
물론 a,b는 다른 값을 가질 수 있다.a=0,b=1일 경우는 어떨까? 앞서 처럼 급속히 발산되는 대신에 (-1,0)과 (-1,1)과 (0,-1)을 반복하는 주기 2에 고착된다.
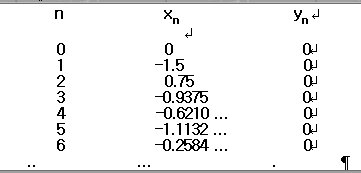
이제 보다 복잡한 a=-1.5.b=0일 경우를 보자.이 계산의 결과는 아래와 같다.
이 값은 선행값으로 되돌아가지 않으면서 x축상의 -1.5와 0.75사이를 이리저리 오가고 있다.이동의 범위는 제한되어 있으면서도 혼돈적이다.
이 사례들에서 우리는 무한으로 탈출하는 운동,주기적인 순환운동,혼돈적 거동 등 여러 가지 흥미로운 거동들을 볼 수 있다.임의의 (a,b)를 변환기(만델부로트 공식)속에 넣어 그 결과를 가지고 다음과 같이 표시해보자.만일 그 값이 x,y축의 원점을 중심으로 반경2의 범위내에 있다면 검은색으로 칠하고 그 밖에 있다면 흰색으로 칠하자.이렇게 해서 구성된 것이 유명한 만델부르트의 우물이다.이것은 다음과 같이 정리할 수 있다.
1.(x,y)평면상에 원점을 중심으로하는 반경2의 원을 그려라.
2.-2에서 2사이의 임의의 점(a,b)를 취하라.
3.계산의 최대횟수를 정하라.
4.(a,b)를 변환기에 넣어 계산을 수행하라.
5.만일 허용된 횟수안에 범위를 벗어나지 않는다면 검은 색으로 칠하라.
6.범위 밖으로 벗어난다면 흰색으로 칠하라.(사실 이것은 단순화시킨 것이며 만델부로트우물을 만들 때는 탈출속도에 따라 다른 색을 부여한다.물론 색의 부여는 전적으로 임의적인 것이다.)
앞의 사례에서 6회째 계산에서 그것이 반경2의 범위내에 있는 것을 확인할 수 있었지만 경우에 따라서는 지금까지의 계산으로는 범위내에 있다고 해도 계산횟수를 늘여가면 그 범위를 넘어가 버릴지도 모른다.사실 회수를 늘여갈수록 만델브로트 우물(검은 부위)은 둥그럼한 형태에서 잘룩한 허리를 가진 형태로 변해간다.
<그림6>연산횟수를 증가시켜감에 따라 만델브로트 우주는 점점 잘룩한 형태로 되어간다.
앞서 만델브로트 변환기를 아래와 같이 나타내었다.
이제 이것이 어디서 도출되어 나오는가를 검토해 보자.
사실 이것은 복소수공간에서
의 사상(mapping)이다.
라할 때
에 이 값을 대입하면,
그러므로 (1)과 (2)는 복소수공간에서
이 관계를 이용하여 QBasic언어로 프로그램하면 다음과 같다.
SCREEN 10
FOR i=1 TO 300
FOR j=1 TO 150
a= -2 + 4*i/300 ← c = a +bi에서 a,b의 움직이는 범위
b= 2 -4*j/300 ←
x = 0 ←초기값을 0으로 한다.
y = 0 ←
FOR n = 1 TO 30←Z30까지 계산
x1 = x * x - y * y + a
y1 = 2 * x * y + b
z = x * x + y * y
IF z 〉4 THEN GOTO 10
x = x1
y = y1
NEXT n
PEST(i,j)
PEST(i,300-j)
10 NEXT j
NEXT i
END
이것을 구동시키면 다음과 같은 만델부로트의 우물이 출력되어 나온다.
<그림7>
만델브로트 맵의 식
를보면 로지스틱 맵의 특수한 형태인
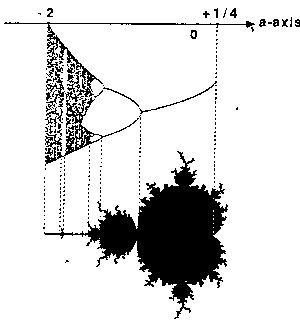
와 동형이라는 것을 알 수 있다.만델브로트 맵은 로지스틱 맵의 2차원 형태이다. 다음 그림은 그 둘 사이의 동형성을 잘 보여준다. 만델브로트 우물에서 큰 혹과 작은 혹간의 가로길이 간의 비는 바로 앞서 찾았던 파이겐바움수라는 것은 아주 인상적이다.
<그림8>갈래질 길이간의 비율이 로지스틱맵과 만델브로트우주에서 동일함에 주목하라.
경계 탈출의 속도의 정도에 따라 색을 달리 배정함으로써 우리는 화려하고 현란한 만델브로트 우주를 얻을 수 있다. 이것의 실행을 보여주는 애플릿이 있다.이제 이것을 이용해서 만델브로트의 우주로 깊숙히 들어가 보자.
http://home.t-online.de/home/eckhard.roessel/
<그림9>만델브로트 우주의 한 모습