
등각나선과 생명의 아름다움(1)
D'Arcy Wentworth Thompson의 On Growth And Form(1919) 중심으로
1.gnomon
소라와 같은 연체동물의 성장방식은 우리와는 다르다.어린이는 전체가 일정한 비율로 커지면서 성인으로 성장한다.(물론 각 부분간의 성장비율을 달리하기 때문에 완전히 닮은 꼴은 아니다.여기에 대해서는 잡기장안의 크기와 형태 참조)그러나 소라의 성장방식은 이와는 다르다.벽돌을 쌓듯이 부분들을 계속 중첩시켜가면서 성장한다.그런데 이것이 중첩되는 방향은 모든 방향에서가 아니고(이것은 소라와 같은 외골격 동물의 경우 가능하지 않다) 오직 한 방향에서만 일어난다.그러면 모양이 달라져야 한다.예컨대 정사각형을 계속 한 방향으로 포개가면 모양은 세로가 계속 길어져서 성장에 따라 모양이 계속 변해갈 것이다.그러나 소라는 성장에 따라 그 모양을 일정하게 유지한다.어떻게 해서 이것이 가능한 것인가?
논의를 간단히 하기위해서 2차원상에서 이 문제를 검토해 보자.적어도 몇가지 가능한 경우가 있는데 이것이 그리이스 철학자들이 비상한 관심을 가져왔던 gnomon (아리스토텔레스는 이것이 피타고라스에 의해서 처음으로 논의되었다고 말하고 있다)이다.
그 가운데 하나가 정방수(square number)이다.이것은 다음과 같다.

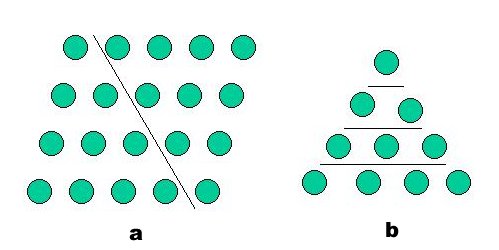
4개의 점으로 정방수를 표현하면 a와 같다.우리는 이것을 좌측의 한점에 3개의 점을 부가한 결과로 해석할 수 있다.(그림b)이 3개의 점이 부가되었지만 원래의 1개의 점과 똑같은 정방형을 이루고 있다.부가되었음에도 원형을 그대로 유지하게 하는 수를 gnomon이라고 한다.여기서 b의 gnomon은 3이다.이 b에 다시 5개의 점을 부가해도 원형을 그대로 유지한다.c의 gnomon은 5이다.(그림c)
우리는 여기서 다음과 같은 것을 알 수 있다.1,3,5,7,..인 홀수열의 각수가 정방형의 gnomon을 형성하고 그것의 합 1,1+3,1+3+5,1+3+5+7,...은 제곱수이고 그 합(점의 개수)은 항의 개수(여기서 변의 점의 수)의 제곱이라는 것을 알수 있다.그래서 1+3+5+...+9의 합은 5의 제곱 즉 25라는 것을 즉각 알 수 있다.일반적으로 홀수열의 합은 그 항의 수의 제곱으로 S=n2으로 나타낼 수 있다.
똑 같은 방법으로 gnomon을 사용하여 짝수열의 합의 일반식을 구할 수 있는데 이것을 피타고라스는 장방수(oblong number)라고 불렀다.

최초의 2에 4,6,8,10,..을 부가해가도 원형이 변하지 않는다.그러므로 이 장방형의 gnomon은 짝수라는 것을 알수 있다.그리고 이 짝수의 합의 일반식은 S=n×(n+1)이라는 것을 위 그림을 통해서 쉽게 알 수 있다.그렇다면 자연수의 합은 어떻게 될까?
위 그림을 보면 알 수 있듯이 이 장방형을 대각선으로 이분했을 때 그 반에 해당한다.장방형을 이분한 그 반을 보면 1+2+3+...의 자연수의 합이라는 것을 알 수 있다.그러므로 자연수의 합은 앞서 짝수의 합 n(n+1)을 2로 나눈 것 즉 S=n(n+1)/2라는 것을 즉각 알 수 있다.이 반을 떼어 놓은 것이 그림b이다.1에 순차적으로 2,3,4를 더해가면 그 형태를 그대로 유지하는 삼각수가 만들어진다.그러므로 자연수는 삼각수의 gnomon이라는 것을 알 수 있다.
곡선의 경우 gnomon이 있는가?그 답은 소라나 조개와 같은 연체동물이 그 해답을 제시해주고 있다.오직 그 외는 解가 없다는 것이 자연이 보여주는 심오한 귀결이기도 하다.여기에 대해서도 그리이스인들은 비상한 흥미를 가졌던바 그것이 바로 황금분할(golden proportion)이다.벽돌을 성장의 말단부위에서 계속쌓아 올려가면서 전체 형태를 유지할 수 있는 유일한 해는 황금분할의 방법 뿐이다.자연은 이것 보다는 보다 연속적 증분량을 사용함으로써 보다 많은 해를 찾아내고 있다.그것이 바로 유명한 등각나선(equiangular spiral)이다.
2.황금비,피보나치수열 그리고 등각나선
우선 보다 간단한 황금분할의 gnomon을 찾아보자.

먼저 길이1의 정사각형에 또 하나의 길이 1의 정사각형을 붙인다.물론 이때 가로 세로의 비는 1:2가 되어 선행한 형태(정사각형)와는 다르다.여기에 다시 길이 2의 정사각형을 붙인다.이제 가로,세로의 비는 3:2가 되어 다시 선행한 형태와는 다르다.다시 길이 3의 정사각형을 덧붙인다.이제 비는 5:3이 된다.다시 5의 정사각형을 덧붙이면 비는 8:5가 된다.계속 가로,세로의 비가 변하므로 gnomon이 없어 보인다.그러나 이 조작 과정을 계속해가면 놀랍게도 두 변의 비는 1:1.618033...에 접근해간다.이것이 황금분할이다.

이것을 도표로 나타내면 그 의미가 분명히 드러난다.
앞서의 조작으로 만들어낸 수인 1,1,2,3,5,8,13,21,....이것이 위도표의 x축에 표시되어 있고 뒷항을 앞항으로 나눈값이 y축에 표시되어 있다.이 x축의 값이 유명한 피보나치수열(Fibonacci Number)인데 1,1에서 시작해서 앞의 두항을 더함으로 다음 항의 값이 생성되고 있음을 알수 있다.
이 도표에서 보면 8회째의 부가 이후 거의 두변간의 비의 변화가 없는 것을 알 수 있다.피보나치수열의 두수간의 비율은 황금비로 수렴하고 있다.그러므로 피보나치수열이 1:1.618033..의 일정비를 만들어내는 gnomon임을 알 수 있다.이 피보나치수열이 만들어내는 것이 등각나선이다.다음 그림은 그것을 보여주고 있다.
피보나치수열이 만드는 등각나선을 보기위해서 위 그림을 클릭하세요
여기서 처음 시작에서는 그렇지 않지만 몇회 정도의 조작이 있은 다음에는 어떤 부분을 잘라도 전체와 같은 모양을 취하고 있음을 알수 있다.
물론 피보나치수열에 의한 것 보다
완벽한 gnomon을 얻어내는 방법이 있다.두변을 1:0.618..로 된 사각형을 그리고 거기에
한변이 1인 정사각형을 부가하고 다시 거기에 한변이 1.618...인 정사각형을 부여하는
등의 방식으로 계속하면 완벽한 gnomon을 얻을 수 있을 것이다.무리수를 허용한다면
이 보다 더 쉬운 방법이 있다.두변이 1: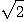

그러나 자연은 무리수를 허용하지 않는다는 점을 주목하자.자연의 설계는 어떤 크기로 떨어져야한다.그런 조건을 부여한다면 유일한 해법은 피보나치수열 밖에 없다는 것을 알 수 있다.
그러나 그 gnomon이 꼭 정사각형일 필요는 없다.크기가 달라져도 일정한 닮은 꼴을 형성하고 있으면 그것은 gnomon으로서 역할을 할 수 있다.자연이 보여주는 것은 바로 이러한 형태의 gnomon이며 여기서 피보나치수열에 입각한 등각나선에 한정되지 아니한 다양한 형태의 나선을 표현하는 것이 가능하다.이것으로 해서 자연에서의 성장의 단위는 연속량이 아니지만 연속량으로 근사적으로 다룰 수 있다.이것을 수학화한 것이 등각나선이다.이 등각나선은 자연의 설계에 대한 깊은 통찰을 던져준다.
3.등각나선
등각나선은 나선이지만 모든 나선이 등각나선은 아니다.이 등각나선이 무엇인가에 대한 직관상을 얻기위해서는 다른 나선과 비교해 보는 것이 유용하다.그 가운데 하나가 아르키메데스나선이라는 것이 있다.여기에는 감아놓은 밧줄이나 시계태엽,두루말이 화장지 그리고 유전정보를 저장하고 있는 이중나선(double helix)등이 있다.이것들은 등각나선이 아니다.이 둘의 차이를 이해하기 위해서 아래 그림을 보자.


2장의 긴종이테이프를 준비하고 하나는 1,2,3,4,5,6,..의 길이(그 단위가 무엇이라도 좋다)가 되도록 표시를 하고,다른 하나는 1,1,2,3,5,8,...의 길이가 되도록 표시를 하자.그 다음 표시한 곳에서 90도로 꺽으면서 접어나간다.이것이 보여주는 모양의 차이는 어떨까?상단의 그림은 이 차이를 보여주고 있다.
이것을 정확히 표현한 것이 아래 그림이다.


아르키메데스 나선 등각나선
아르키메데스나선의 경우 각 코일들간의 간격이 일정한데 대해서 등각나선의 경우 코일들간의 간격이 기하급수적으로 증가한다.전자의 경우 그것의 증식은 외부로부터 오며 선행항에 그것이 덧붙여진다.등각나선의 경우 내부로부터 성장해가는 것이며 아무것도 바깥에서 덧붙여진 것이 아니다.이것은 자기증식의 본질로서 생명체의 성장과 닮아있다.
아르키메데스 나선은 다음과 같이 정의된다."반경벡터가 극좌표의 극점O 주위를 일정한 속도로 운동하고 있다면 그위를 일정한 속도로 운동하고 있는 점p가 그리는 궤적이 아르키메데스나선이다."
반경을 r(OP)이라고 하면 이 거리는 일정한 속도a에 전체 회전수 즉 회전각θ를 곱한 것이다.즉 r=aθ로 나타낼 수 있다.한번 회전할 때 마다 반경r이 일정하게 늘어나고 있음을 이 식에서 알 수 있다. 반경r은 등차수열적 증가를 보여준다.이 나선의 특징은 회전수가 증가함에 따라 처음의 모양이 어떠했든 상관없이 원을 닮아간다는 점이다.이것은 우리가 돗자리를 감아가면 처음 모양에 상관없이 원형을 닮아간다는 것을 통해서 쉽게 이해할 수 있다.이것은 곡선에 그은 접선이 90도에 수렴할 때 까지 계속 변해간다는 것을 의미한다.반면 등각나선의 경우 그 회전수에 관계없이 접선의 각도가 일정하다.(여기서 등각나선이란 말이 나왔다)
각 α는 항상 일정하다.그림을 클릭하면 동화상을 통해 등각이 등각나선을 만드는 이유를 시각적으로 이해할 수 있습니다.
점p가 일정한 속도로 이동하는 대신 "극점O에서의 거리에 따라 속도가 증가하는 방식으로 이동한다면 그것이 그리는 궤적은 등각나선이다."그래서 코일간의 간격은 일정한 비율로 선행회전에서의 코일간의 간격 보다 길어진다.(아르키메데스나선의 경우 회전수에 관계없이 코일간의 간격은 일정하다) 말하자면 반경벡터는 등비수열적으로 길어진다.이것은 r=aθ로 표기할 수 있다.아르키메데스 나선의 경우 반경은 회전할 때마다 a를 2로 두었을 경우 길이가 2,4,6,8의 비율로 증대하지만 등각나선의 경우 4,16,64.256.로 증가한다.그래서 전자의 경우는 코일간격이 2로 항상 일정하지만 후자의 경우는 회전에 따라 코일간의 간격이 12,48,192..로 급격히 벌어진다.
아르키메데스 나선은 아르키메데스라는 그 이름에서 알 수 있듯이 고대로부터 잘 알려져 있었다.그러나 이 등각나선을 발견하고 황금나선은 이것의 특수한 경우라는 것을 밝힌 사람은 데카르트였다.
이 나선의 가장 큰 특징은 임의의 점 p에서 그 나선에 그은 접선과 반경벡터가 만나서 이루는 각이 항상 일정하다는 것이다.그리고 코일간의 간격의 등비수열적 증가는 이 등각이라는 조건이 만들어내는 결과이기도 하다.그러므로 반경벡터와 이 각도간의 관계식에 이 등각나선의 본질이 응축되어 있다.이제 이것을 도출해 보자.

이 식에서 보듯이 등각나선에는 두가지 중요한 상수(자연주의자의 용어로 특이성)가 있는바 하나는 나선의 각의 크기 즉 상수각 α이고,다른 하나는 회전각 θ에 대한 반경벡터의 증가율이다.
이 식이 가지는 의미에 대한 직관상을 갖기위해서 이상적 등각나선을 보이는 앵무조개(Nautilus)의 경우를 보자.아래 그림을 그것을 보이고 있다.
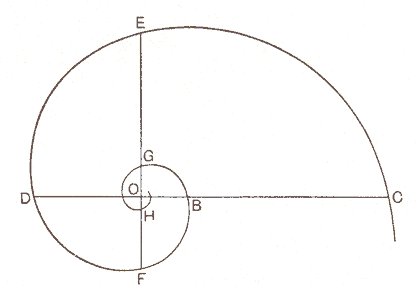
여기서 우리는 이 나선의 임의의 두 점에 대해서 그것의 반경벡터의 크기r 또는 나선의 코일간의 폭 w를 측정할 수 있다.그러면 비교되고 있는 두 점의 반경벡터 또는 폭간에는 다음 관계가 성립한다.
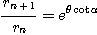

비교를 위해서 한쪽의 반경 또는 코일의
폭을 1로 잡으면 위식은 단순히 
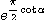

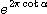
각α의 결정은 비교적 간단한데 나선상의
임의의 두 반경r1,r2의
길이의 비가 곧 
r=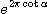
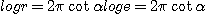

우리는 등각나선의 위상차에 따른 r의 값의 차이를 통해 상수각 α의 값을 구할 수 있다.이렇게 해서 구한 값이 아래 도표에 나와 있다.
r/1 |
α |
1.1 |
89。 8' |
1.25 |
87 58 |
1.5 |
86 18 |
2.0 |
83 42 |
2.5 |
81 42 |
3.0 |
80 5 |
3.5 |
78 43 |
4.0 |
77 34 |
4.5 |
76 32 |
5.0 |
75 38 |
10.0 |
69 53 |
20.0 |
64 31 |
50.0 |
58 5 |
100.0 |
53 46 |
1000.0 |
42 17 |
10,000.0 |
34 19 |
100,000.0 |
28 37 |
1,000,000.0 |
24 28 |
10,000,000.0 |
21 18 |
100,000,000.0 |
18 50 |
1,000,000,000.0 |
16 52 |
우리는 이 간단한 표로부터 몇가지 흥미있는 것을 알아낼 수 있다.앵무조개의 경우 선행코일과 후행코일간의 폭의 차이는 약 3이다.이것은 선행코일을 1로 한다면 후행코일의 폭은 3이라는 것을 의미하고 여기서 r=3이다.이 앵무조개의 곡선의 만곡의 상수각은 얼마일까? 앞의 식에 r=3을 대입하면 그 각은 약 80도 정도라는 것을 계산할 수 있다.
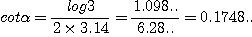
로그표에서 이 값에 해당하는 α값을 찾으면 80도 정도이다.앵무조개나 암모나이트처럼 나선으로 돌돌말려 성장하는 연체동물의 종류는 보통 이 각이 80도와 85도 사이에 있다.위의 표에서 볼 수 있듯이 80도 보다 작아지면 코일 사이의 폭이 점점 커져(다시말해서 r의 값이 커져) 나선으로서의 외양을 점점 잃어가게 된다.예컨대 어떤 코일의 길이가 1cm이고 나선각이 80도라면 r=3이기 때문에 다음 코일의 폭은 3cm 정도가 되고 다음은 9cm가된다.그러나 그 각이 70도라면 다음 코일의 폭은 10cm,그 다음 코일은 100cm 즉 무려 1m로 늘어난다.각이 28도가 되면 어떻게 될까? r이 무려 100,000이기 때문에 다음 코일의 폭은 1km,그 다음은 무려 10만 km가 된다.17도가 되면 처음 코일의 1cm가 다음에는 1만 km가 된다.1cm에서 시작한 조개가 다음 코일에서는 지구를 벗어나 우주로 뻗어나간다! 아래 그림은 각도의 차이에 따른 형태의 차이를 도식적으로 보여주고 있다.

물론 조개가 이렇게 무한대로 성장할 수는 없다.대합과 앵무조개는 등각나선이라는 동일한 설계에 기초하고 있다.그러나 대합의 경우 그 만곡의 각도가 작아서 가시적인 나선을 보이기 전에 성장이 종료된다.그래서 우리는 대합에서 등각나선이 아닌 완만한 곡선만을 보게 되는 것이다.사실 우리의 치아나 동물의 발톱도 등각나선의 설계를 따르고 있지만 그 각이 40도 이하여서 거의 구부러진 원통처럼 보이는 것이다.연체동물에도 이런 종류를 찾아볼 수 있다.
우리는 생명체들의 다양한 형태에도 불구하고 그 근저에 흐르고 있는 보편적 설계원리가 있으며 그 하나가 등각나선이라는 것을 확인할 수 있었다.그리고 gnomon,황금분할,등각나선 등에 수학자,철학자,생물학자들이 그렇게 매료되어온 이유를 확인할 수 있었다.그것은 바로 생명이 자기자신을 만들어가는 디자인이었다.
4.넷상에서 등각나선 연습하기
우리는 등각나선의 수학적 특성을 이해하는데 그 목적이 있는 것이 아니라 생명의 기본설계가 자연속에서 어떻게 구체화되고 있는가에 대한 느낌을 얻고자는데 있다.수학적 추론을 끌고 온 것도 이 최소한의 목적을 달성하기 위한 것이었다.이제 수학은 잊어 버리고 각α의 변화에 따라 등각나선의 형태가 어떻게 변해가는지를 실제 변수를 바꿔가면서 그려 보는 것이 가장 효율적이다.
이 연습공간을 제공하는 사이트가 있다.이 사이트에 들어가면 다음과 같은 애플릿이 나온다.변수를 바꿔보면서 나선의 형태의 변화에 대한 감을 가져보도록 하자.(이 그림을 클릭하세요)
지금까지 등각나선에 대해서 논의해 왔지만 이것은 자연이 보여주는 나선의 2차원 그림자일 뿐이다.앵무조개 처럼 거의 평면상의 성장을 보이는 것도 있지만 대부분의 소라와 고동은 이 등각나선을 3차원 상에서 구현한다.자연의 아름다움을 이해하기 위해서 이제 우리는 등각나선의 3차원적인 적용을 검토해 보아야 한다.
1962년 데이비드 라우프(D.Raup) 가 컴퓨터를 이용해서 등각나선의 3차원상을 구현하고 이것이 실제 자연속에 존재하는 연체동물들과 얼마나 닮았는지를 보여줌으로써 깊은 인상을 남겼다.("Computer as aid in describing form in gastropod shells",1962)그는 심지어 자연계에서 찾아볼 수 없는 형태를 만들어내기도 했다.그것은 가능한 형태이기 때문에 과거에 아마 존재했을지 모르며 아니면 미래에 만들어질지도 모른다.
최근 이 라우프의 논의를 도킨스가 그의 저서 Climbing Mount mprobable (1997)에서 대중화시켰다.다음번에 이 도킨스의 모델을 정리해서 올리고자 한다.



